����A�������Ȋw�T��@���e�L�X�g5��
�@�d���������́C�\�v�Z�\�t�g�ƌĂ�Ă��镪��̃\�t�g�ł��D�����ł͐��w
�ł̊��p�i�u���w�a�v�R�́@���v�ƃR���s���[�^�j�𒆐S�Ɋw�K���Ă����܂����C
���̃\�t�g�̊��p�͈͂͑�ύL���C���낢��ȕ���Ŋ��p����Ă��܂��D
�P�D�d������������
�E �f�[�^�̍쐬
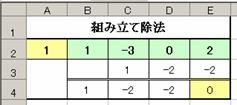
�����K�P���@���ȏ����y�����P�z�`�y�����U�z�̍쐬
 �V�[�g����
�V�[�g����
[����]�ɕύX
���āC���ȏ�
�u���w�a�v��
�U�̎���
p.106�`p.121�@
���E�̂悤��
���͂���D
�@�@�@�@�@ �ۑ��ꏊ
�u������ް�ցv
�@�@��
�uWORK�v
�@�@��
�uExcel�v
���V�K�쐬��
�@�@��
���v����
���t�@�C������
(1) �x�����z
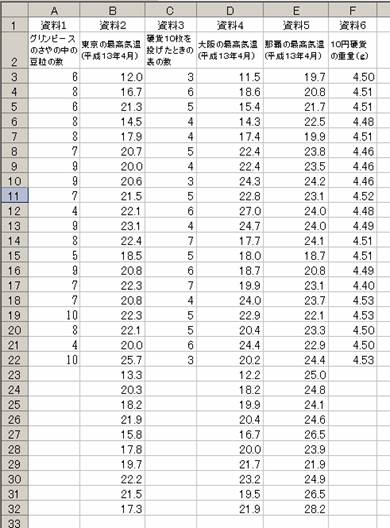
 �����K�Q���@�y�����P�z�̓x�����z�\
�����K�Q���@�y�����P�z�̓x�����z�\
�@�@�@�@�@�@�V�[�g����[�x�����z]�ɕύX����
�@�@�@�@�@���̂悤�ȓx�����z�\���쐬����D
�@
�@�@�@�@�@�@���@�x���̌v�Z�́C���icountif�j
�@�@�@�@�@�@�@�@���g���Ɗy�ɂł��܂��D
�@�@�@�@�@�@�@�@�g�����ɂ��ẮC���j���[�o�[
�ɂ���k�w���v(H)�l�Œ��ׂĂ��������D
����P��
�y�����R�z���d�݂P�O���𓊂����Ƃ��̕\�̐����̓x�����z�\
�i���Γx����t����j���V�[�g[�x�����z]�ɍ쐬����D
�����K�R���@�y�����Q�z�̓x�����z�\
 �@�V�[�g[�x�����z]��
�@�V�[�g[�x�����z]��
���̂悤�ȓx�����z�\
���쐬����D
�@�@�@�@�@�@���@�K���l�́A�K��
�@�@�@�@�@�@�@�@�̋��ɑ�
�āC���iint�j
���g���悤�ɂ�
��������.
�܂��C�x���ɂ��ẮC���ifrequency�j���g���Ă��������D
�g�����ɂ��ẮC���ȏ�p.113�ɂ��ڂ��Ă��܂�.
����Q��
�y�����S�z�����̍ō��C���i�����P�R�N4���j���̓x�����z�\
�i���Γx����t����j�V�[�g[�x�����z]�ɍ쐬����D
����A�������Ȋw�T��@���e�L�X�g6��
(2) �q�X�g�O����
�����K�S���@�y�����P�z�̃q�X�g�O�����Ɛ܂���O���t
�@�@�@�@�@�@�V�����V�[�g�i�V�[�g����[�q�X�g�O����]�j�Ɏ��̂悤�ȃq�X�g�O������
�쐬����D�܂��C�O���t�̎�ނ��u�܂���v�ɕύX����D
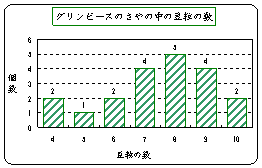
����P��
�y�����R�z���d�݂P�O���𓊂����Ƃ��̕\�̐����̃q�X�g�O����
�@�@�@�@�@���V�[�g[�q�X�g�O����]���쐬����D
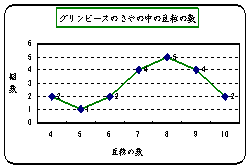
�����K�T���@�y�����Q�z�̃q�X�g�O�����Ɖ~�O���t
�@�@�@�@�@�@�V�[�g[�q�X�g�O����]�Ɏ��̂悤�ȃq�X�g�O�����Ɖ~�O���t���쐬����D
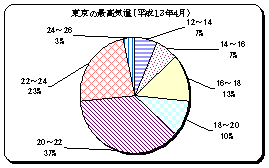
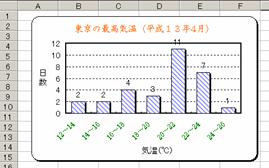
����Q��
�y�����S�z�����̍ō��C���i�����P�R�N4���j���̃q�X�g�O��
���Ɖ~�O���t���V�[�g[�q�X�g�O����]�ɍ쐬����D
(3) �U�z�}�i���}�j
�@�@�@�@�@�Q�̃f�[�^�n��̊W���ׂ�̂ɎU�z�}�i���}�j������܂��D�f�[�^
�@�@�@�@����������E��ɂ����ĎU����Ă���Ƃ����̑���������Ƃ����C���ォ��
�E���ɂ����ĎU����Ă���Ƃ������̑���������Ƃ����܂��D�f�[�^������
�Ȃ��U����Ă���Ƃ��͑��ւ��Ȃ��Ƃ����܂��D
�����K�U���@�y�����Q�z�Ɓy�����S�z�̑��}
�@�V�����V�[�g�i�V�[�g����[���}]�j�Ɏ��̂悤�ȁy�����Q�z�Ɓy�����S�z
�̑��}���쐬����D
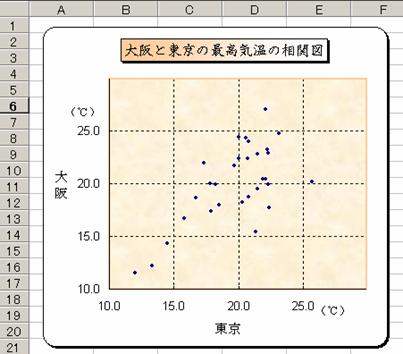
����R��
�y�����S�z�����̍ō��C���i�����P�R�N4���j���Ɓy�����T�z
���ߔe�̍ō��C���i�����P�R�N4���j�̑��}���V�[�g��[���}]�ɍ쐬��
��D�܂��C�����̑��֊W�ɂ��Ă��邩�Ȃ����ׂ�D
����A�������Ȋw�T��@���e�L�X�g7��
(4) ��\�l
�@�f�[�^�S�̂̓�����\�����l���\�l�Ƃ����܂��D
�E���ϒl�@�F�@n�̃f�[�^�@![]() �@�̕��ϒla�́C
�@�̕��ϒla�́C
�@�@�@�@�@�@�@�@![]()
�E���W�A���i�����l�j�F�@�f�[�^���������i�傫���j���ɕ��ׂ��Ƃ��C���Ԃ��^���̒l�D
�������C���������̂Ƃ��́C�^��2�̕��ς��Ƃ�D
�@�@�@�@�@�E���[�h�i�ŕp�l�j�F�@�x�����z�ɂ����ēx�����ł������K���l�D
����P��
���W�A���ƃ��[�h�ɂ��āC�C���^�[�l�b�g�����p���čX�ɏڂ�
�����ׂ�D
�����K�V���@�y�����U�z�i�@�P�O�~�d�݂̏d�ʁ@�j�̕��ϒl
�y�����U�z�̕��ϒl����̎���Excel�̊��iAverage�j���g���Q�ʂ�̕�
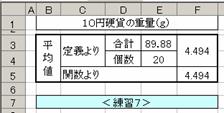 �@�ŋ��߂�D���̂Ƃ��C�����U�̃f�[�^��
�@�ŋ��߂�D���̂Ƃ��C�����U�̃f�[�^��
���O�i�����U�j��t���Ċ��𗘗p����D
�������C�V�����V�[�g���i�V�[�g����
[��\�l]�j�쐬���āC����Ɏ��̂悤��
�L�q����D
�@�@�@�@�@�@�i�g�p������FSum�CCount�CAverage�j
�@�@�@�@�@�@���@�Z���͈͂ɖ��O��t������@
�@�@�@�@�@�@�@�@�k�}��(I)�l���k���O(N)�l���u��`(D)�v
����Q�� �y�����Q�z�̕��ϒl����̎���Excel�̊��iAverage�j���g��
�Q�ʂ�̕��@�ŋ��߂�D
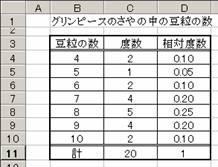
�����K�W���@�x�����z��蕽�ϒl�����߂�
�@�y�����P�z�i�O�����s�[�X�̂���̒��̓����̐��j�̕��ϒl��x�����z��苁
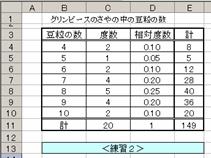 �߂�D�܂��C���̒l�Ǝ��ۂ̕��ϒl�Ƃ��r����D
�߂�D�܂��C���̒l�Ǝ��ۂ̕��ϒl�Ƃ��r����D
���̂Ƃ��C�����K�Q���̓x�����z�ɗ�i�v�j���P��
 �lj�����D
�lj�����D
����R�� �y�����Q�z�y�����R�z�y�����S�z�����ϒl���x�����z��苁�߂�D
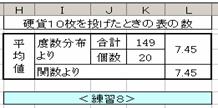
 �����K�X���@�y�����U�z�̃��W�A�������߂�
�����K�X���@�y�����U�z�̃��W�A�������߂�
�@�@�@�@�y�����U�z�i�P�O�~�d�݂̏d�ʁj�̃f�[�^����בւ���
���W�A�������߂�D�܂��CExcel�̊��iMedian�j��p����
���߂��l�œ������킹������D
�������C���בւ�������Ƃ��ɂ̓V�[�g�i�����j�̕��ʂ�
���āi�V�[�g���F�u���� (2)�v�j�C���̃V�[�g�ōs�����ƁD
 �@�@�@�@���@���בւ����i�\�[�g�j
�@�@�@�@���@���בւ����i�\�[�g�j
�@�@�@�@�@�E���בւ���f�[�^�͈͂��w�肷��D
�@�@�@�@�@�E�k�f�[�^(D)�l���k���בւ�(S)]
�@�@�@�@�@�@���k���ݑI�����Ă���͈͂�������בւ���l
�@�@�@�@�@�@���k�������~����I������l
����S�� �y�����P�z�`�y�����T�z�ɂ��Ă����W�A�������߂�D
����T�� �@�����K�Q���Ɓ����K�R���ō쐬�����x�����z�\�̃��[�h�����߂�D
����A�������Ȋw�T��@���e�L�X�g8��
(5) ���U�ƕW����
�@���U��W�����́C�f�[�^�̎U���̓x�����𑪂�w�W�Ƃ��Ďg����D
n�̃f�[�^�@![]() �@�ɂ��āC���ϒl��a
�Ƃ���ƁC
�@�ɂ��āC���ϒl��a
�Ƃ���ƁC
�E�@���U�F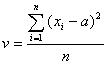
�@�@![]() �@����@�@
�@����@�@
�E�@�W�����F![]()
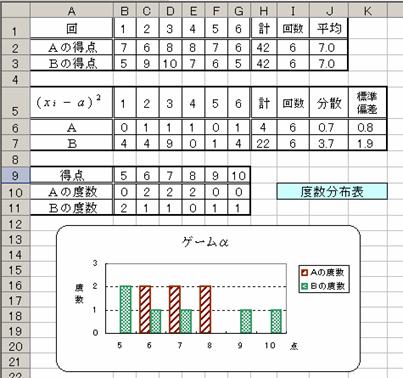
�����K�P�O���@�ϗʂ̕��U�ƕW����
���̕\�͂`�C�a�Q�l��10�_���_�̃Q�[�������U��s�������ʂł���D���̂悤��
�q�X�g�O�������쐬����D�܂��C���ςƕ��U�y�ѕW���������߂�D
���U����v�Z�i�e�X�g�Ȃǁj�ōs���Ƃ��C���ς������ł���·@�̎���p����
�v�Z���C�����łȂ���@![]() �@�Ōv�Z��������ȒP�ł���D
�@�Ōv�Z��������ȒP�ł���D
����P��
�@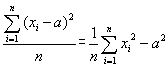 �ƂȂ邱�Ƃ������D
�ƂȂ邱�Ƃ������D
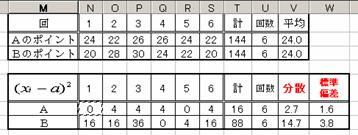
�����K�P�P���@�ϗʂ�ϊ������Ƃ��̕��U�ƕW����
�@�����K�P�O���̃Q�[�����ɂ����āC���_x�ɑ���![]() �|�C���g���炦���
�|�C���g���炦���
���C�`�̂��炦��|�C���g�̕��ϒl�ƕ��U�y�ѕW���������߂�D
�@�@�@�@��ʂɁC�ϗ�x�ɑ��āC�V�����ϗ�y��![]() �ic�Cd�͒萔�j�ł���
�ic�Cd�͒萔�j�ł���
�Ƃ��C�ϗ�y�̕��ς́@![]() �C���U�́@
�C���U�́@![]() �@�ƂȂ�D
�@�ƂȂ�D
�@�������C![]() �C
�C![]() �͕ϗ�x�Cy�̕��ρC
�͕ϗ�x�Cy�̕��ρC![]() �C
�C![]() �͕ϗ�x�Cy�̕��U�ł���D
�͕ϗ�x�Cy�̕��U�ł���D
����Q��
�@���2�̊W��![]() �C
�C![]() �����藧���Ƃ������D
�����藧���Ƃ������D
Excel�ɂ́C���U�iVarp�j�ƕW�����iStdevp�j�����߂��������܂��D
����R�� �@�����K�P�O�������K�P�P���̕��U�ƕW��������Varp��
Stdevp��p���ċ��߂�D
����A�������Ȋw�T��@���e�L�X�g9��
(6) ���W��
���W���́C�Q�̕ϗ�x�Cy�̊W�̓x�����𑪂�w�W�Ƃ��Ďg����D
�ϗ�x��n�̃f�[�^�@![]() �@�����ϒl��
�@�����ϒl��![]() �C
�C
�ϗ�y��n�̃f�[�^�@![]() �@�����ϒl��
�@�����ϒl��![]() �Ƃ���ƁC
�Ƃ���ƁC
�E�����U�F�@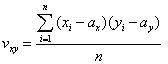
�@�@�@�@�@![]()
![]()
�E���W���F�@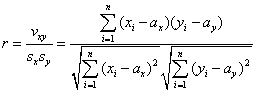
![]() �s�����@
�s�����@![]() ��
��![]()
���V�������c�̕s�����Ƃ����D
���ؖ����@���ׂĂ̎���t�ɑ��āC![]() ��0�@����������D
��0�@����������D
�@�@�@�@�@�V�������c�̕s�������C���W��r�̂Ƃ�͈͂́C-1 �� r �� 1 �ƂȂ�D
�܂��Cr�� 1�ɋ߂��قǐ��̑��ւ������Ƃ����C-1�ɋ߂��قǕ��̑��ւ�����
�Ƃ����D
�����K�P�Q���@�����K�P�O���̂`�̓��_��ϗ�x�CB�̓��_��ϗ�y�Ƃ��āCx��
y�̋����U�Ƒ��W�����߂�D�܂��Cx��y�̑��֕\���쐬����D
�i�V�����V�[�g�F�u���W���v���쐬����j
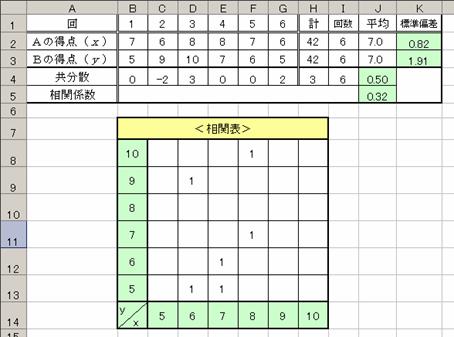
�@����P�S���@���W�������߂�Excel�̊��iCorrel�j��p���ā����K�P�P����
�|�C���g�̑��W�������߂�Ɓ����K�P�O���̑��W���Ɠ����ƂȂ�D
�@���̗��R����D
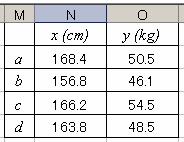
�@�@�@����P�T���@�S�l�̐��ka�Cb�Cc�Cd ��
�g�� x�icm�j�Ƒ̏d y�ikg�j���E�̂悤
�ł������D
x��y�̋����U�Ƒ��W�������߂�D
�܂��Cx��y�̑��֕\���쐬����D
����A�������Ȋw�T��@���e�L�X�g10��
Excel�ł́CVisual Basic for Application(VBA)�Ƃ����v���O���~���O���ꂪ
�g���܂��D������g���ăv���O���~���O�̊�b���w�K����ƂƂ��ɁC���̊��p�@
�ɂ��Ă��w�K���Ă����܂��D
(1)
�R�}���h�{�^���ƃv���O����
�R�}���h�{�^�����N���b�N����Ƃ���Ɋ��蓖�Ă��Ă���v���O��������
�s���܂��D
�����K�P�R���@�R�}���h�{�^���Ƀv���O������ݒ肷��
 �@�E�R�}���h�{�^�������[�N�V�[�g��ɐݒ肷��D
�@�E�R�}���h�{�^�������[�N�V�[�g��ɐݒ肷��D
�@�@�m�\��(V)�n��[�c�[���o�[(T)]��[�t�H�[��]
�@�@�Ƀ`�F�b�N������D
![]() �@�@�R�}���h�{�^���@�@�@���N���b�N���āC�{�^��
�@�@�R�}���h�{�^���@�@�@���N���b�N���āC�{�^��
 ��ݒu����ꏊ���w�肷��ƁC�}�N���̓o�^��
��ݒu����ꏊ���w�肷��ƁC�}�N���̓o�^��
![]() �E�C���h���\�������̂Ł@�@�@�@�@�@�{�^��
�E�C���h���\�������̂Ł@�@�@�@�@�@�{�^��
�������D
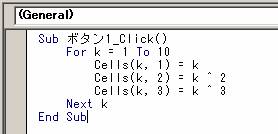
�@�@�@�@�E���W���[���i�v���O�����̒P�ʁj���L�q�����
�ʂ��\�������D�����Ƀv���O�������L�q����D
 �@�@�@�@�@
�@�@�@�@�@
���@�J��Ԃ����iFor �`Next�j
�@�@�@�@�@�@�@�����J��Ԃ��Ƃ��Ɏg�p����Dk�����[�v�ϐ��Ƃ����D
����P�U���@�R�}���h�{�^����̖��O��[�{�^��1]����[�v�Z]�ɕύX����D
�@�܂��C���W���[������[�{�^��1_Click]����[�v�Z]�Ƃ���D
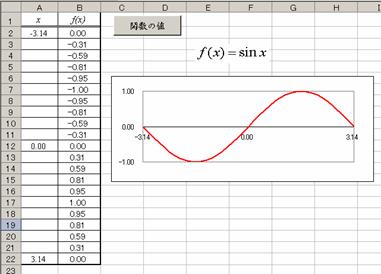
�����K�P�S���@���̃O���t�iy = sin x�j��\��
�Z��(2,1)��[=-PI()]�C�Z��(22,1)��[=PI()]�Ɠ��͂���Ɗe�Z���̒l�������I�ɓ���
����D
 �@�R�}���h�{�^����̖��O��
�@�R�}���h�{�^����̖��O��
���W���[�������Ƃ���[����
�l]�Ƃ���D
�O���t�̓O���t�E�B�U�[�h
���܂����I�����C�f�[�^
�͈͂�[B2:B22]�C���ڎ����x
����[A2:A22]�Ƃ���D
�����W���[����

Sub ���̒l()
s =
Cells(2, 1)
e =
Cells(22, 1)
d =
(e - s) / 20
For
k = 2 To 22�@�@�@�@�@�@���@���iFunction�j
x = s + d * (k - 2)�@�@�@�@�@Module��Function�̈Ⴂ�́C�߂�l����邩
Cells(k, 1) = x�@�@�@�@�@�@�@���Ȃ����̈Ⴂ�݂̂ł��D
Cells(k, 2) = f(x)�@�@�@�@�@ �߂�l�́C������[�߂�l]�Őݒ肵�܂��D
 Next k�@�@�@�@�@�@�@�@�@�@�@�@ �܂��C���W���[������Ɉ����p���ϐ�����
Next k�@�@�@�@�@�@�@�@�@�@�@�@ �܂��C���W���[������Ɉ����p���ϐ�����
End Sub�@�@�@�@�@�@�@�@�@�@�@�@�@��()�̒��ɋL�q���C����������Ƃ����܂�.
![]() Function f(x)�@�@�@�@�@�@�@�@�@�@���D
Function f(x)�@�@�@�@�@�@�@�@�@�@���D
f =
Sin(x)
End Function�@�@�@�@�@�@�@�@�@����P�V���@![]() ��
��![]() �i0��x��2�j
�i0��x��2�j
�̂Q�̃O���t���ɕ\������D
����A�������Ȋw�T��@���e�L�X�g11��
(1)
������
�v���O�����́C�J��Ԃ����Ə������̑g�ݍ��킹�ō���Ă��܂��D�����ł�
�@�@�@�@�������𒆐S�Ɋw�K���܂��D
�E���[�N�V�[�g�ɑg�����@�̎d�g�݂̕\��
�쐬����D
�@�@�@�E�Z��( B2:E2 )�ɂ́C�R���̐����̌W����
���͂���D
�@�@�@�E�Z��( B4 ) ���u = IF(A2="","",B2)�v�Ƃ���ƁC�Z��( A2 ) ���̂Ƃ���
��![�p�ێl�p�`�����o��: �]��](2-1Excel.files/image139.gif) �ƂȂ�C�����łȂ��Ƃ��̓Z��( B2 )�̒l�ƂȂ�D
�ƂȂ�C�����łȂ��Ƃ��̓Z��( B2 )�̒l�ƂȂ�D
�E�Z��( C3:E4 ) �̊e�Z���ɂ͎����L�q����D
�@(�@)�@![]() ��
�� ![]() �Ŋ��������Ɨ]������߂�D
�Ŋ��������Ɨ]������߂�D
�@(�A)�@![]() ��
�� ![]() �Ŋ�����悤��a�̒l���߂�D
�Ŋ�����悤��a�̒l���߂�D
 �����K�P�U���@�Q���������̎�����
�����K�P�U���@�Q���������̎�����
�E�R�}���h�{�^��[�Q���������̎�����] ���쐬���C
���W���[�����쐬����D
�@�@�@�E�Z��( B6:D6 )�ɂQ��������![]() ��
��
�W��a�Cb�Cc����͂���D
�@�@�@�E�O���[�o���ϐ���ݒ肷��D
 Dim a, b, c As Double
Dim a, b, c As Double
Dim r As Integer
�@�@�@�E�Q���������̎����������߂郂�W���[���iSolve2�j���쐬����D

 Sub Solve2()
Sub Solve2()
 �@�@�@a = Cells(r, 2): '�Q���̌W��
�@�@�@a = Cells(r, 2): '�Q���̌W��
�@�@�@b = Cells(r, 3): '�P���̌W��
�@�@�@c = Cells(r, 4): '�萔��
�@�@�@d = b ^ 2 - 4 * a * c
�@�@�@If d >= 0 Then
�@�@�@Cells(8, 3) = (-b - Sqr(d)) /
(2 * a)
�@�@�@Cells(8, 4) = (-b + Sqr(d)) /
(2 * a)
 �@�@�@Else
�@�@�@Else
�@�@�@Cells(8, 3) = ""
�@�@�@Cells(8, 4) = ""
�@�@�@End If
End Sub

�����K�P�V���@�R���������̎�����
�E�O���[�o���ϐ���d��lj�����D
�E���if3�j���쐬����D
�E�R�}���h�{�^��[�R���������̎�����]���쐬���C���W���[�����쐬����D
 Sub Solve1()
Sub Solve1()
�@�@�@�@�@a = Cells(2, 2):b =
Cells(2, 3):c = Cells(2, 4):d = Cells(2, 5)
 �@�@�@�@�@For k = 1 To Abs(d)
�@�@�@�@�@For k = 1 To Abs(d)
�@�@�@�@�@If f3(k) = 0 Then
�@�@�@�@�@Cells(2, 1) = k: k = Abs(d)
 �@�@�@�@�@ElseIf f3(-k) = 0 Then
�@�@�@�@�@ElseIf f3(-k) = 0 Then
�@�@�@�@�@Cells(2,
1) = -k: k = Abs(d)
�@�@�@�@�@End If
�@�@�@�@�@Next k
�@�@�@�@�@r = 4: Solve2
End Sub
����A�������Ȋw�T��@���e�L�X�g12��
(2)
�O���[�o���ϐ�
���W���[���S�̂Ŏg�p�ł���ϐ����O���[�o���ϐ��Ƃ����܂��D
���̕ϐ���ݒ肷��Ƃ��́CPublic����(Declarations)�ɋL�q���܂��D
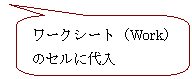
�����K�P�W���@�R�����Ƃ��̓����̃O���t
�E�\�������Ԃ��Z���iB1:C1�j�ɐݒ肷��D
�E��������Ƃ��̑������Z���iB2�j�ɐݒ肷��D
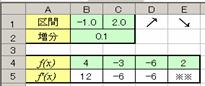
�E�R�����̌W���������̍����ق�����Z���iB4:E4�j�ɓ��͂���D
�E�����̌W�����Z���iB5:D5�j�ɐ����œ��͂���D
�E���̒l�����[�N�V�[�g�i�V�[�g���F�uWork�v�j�ɓ��͂���v���O�������쐬���C
����ɃR�}���h�{�^��[���̃O���t]�����蓖�Ă�D
�@�@�@�E�O���t�E�B�U�[�h�Ő܂���O���t��I�����C�f�[�^�͈͓���ݒ肷��D
![]()

 Sub ���̒l()
Sub ���̒l()
�@�@�@s = Cells(1, 2): e = Cells(1,
3): z = Cells(2, 2)
�@�@�@ For k = 0 To 3: a(k) =
Cells(4, k + 2): Next k
�@�@�@n = 1
 �@�@�@For x = s
To e Step z
�@�@�@For x = s
To e Step z
�@�@�@Sheets("Work").Cells(n,
1) = x
�@�@�@Sheets("Work").Cells(n,
2) = f3(x)
�@�@�@Sheets("Work").Cells(n,
3) = df(x)
 �@�@�@n = n + 1
�@�@�@n = n + 1
�@�@�@Next x
End Sub
(3)
�L�[�}�N��
Excel�ɂ̓L�[�����o�^����@�\������܂��D������L�[�}�N���Ƃ����܂��D
�����ҏW���ăv���O�����̒��ɑg�ݓ���邱�Ƃ��ł��܂��D
�����K�P�X���@�����\�ƃL�[�}�N��
�E�����\���쐬����D
�E�Z���iB10:F12�j�������L�[�}�N�����쐬����D
�@[�c�[��(T)]��[�}�N��(M)]��[�V�����}�N���̋L�^(R)...]
![]() �E���삪�I�������@�@�@�@�@[�L�^�I��(R)]�Ƃ���D
�E���삪�I�������@�@�@�@�@[�L�^�I��(R)]�Ƃ���D
�@�@�@����P�W���@�����K�P�W���̓���
f�f (x) = 0
�ƂȂ�����lx���Z���iB8:C8�j��
�@�@�@�\������v���O�������쐬����D�i�v���O�������F�u�����̉��v�j
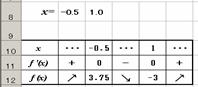
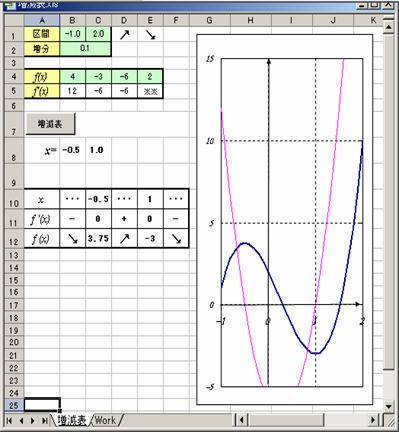
�����K�Q�O���@�R�����̑����\�ƃO���t
�@�R�����̌W����^����Ƒ����\�ƃO���t�i�������܂ށj��\������D

![]() Sub �����\()
Sub �����\()
![]() �@���̒l
�@���̒l
�@�����̉�
�@x1 =
Cells(8, 2): x2 = Cells(8, 3)
�@Cells(10,
2) = "���"
�@Cells(10,
3) = x1: Cells(10, 4) = "���"
Cells(10, 5) = x2: Cells(10, 6) = "���"
�@Cells(11,
3) = 0: Cells(11, 5) = 0
�@If a0 >
0 Then
�@ Cells(11, 2) = "�{": Cells(11, 4) = "�|":
Cells(11, 6) = "�{"
�@Else
�@ Cells(11, 2) = "�|": Cells(11, 4) = "�{":
Cells(11, 6) = "�|"
�@End If
End Sub
�y�ۑ�1�z�@���̖���Excel�̃c�[���u�ۑ�i����2004�j.xls�v�𗘗p���ĉ����D


����A�������Ȋw�T��@���e�L�X�g13��
(1)
With�`End With
�����Ώۂɑ��Ă������̐ݒ������Ƃ��ɁC���̑Ώۂ����̂ǎw�肷
�@�@�@�@��̂��ȗ�����Ƃ��Ɏg�p���܂��D
 �@�@�@���၄�@�@With Selection.Font
�@�@�@���၄�@�@With Selection.Font
.Name
= "�l�r ����"
.Size
= 11
.Strikethrough
= False
.Superscript
= False
.Subscript
= False
.OutlineFont
= False
.Shadow
= False
.Underline
= xlUnderlineStyleNone
.ColorIndex
= xlAutomatic
End
With
�@�@�@����P�X���@�����K�Q�O���̃��[�N�V�[�g�i�����\�j�̃Z���iB10:F12�j�̓��e��
�����āC�t�H���g���u�l�r
�����v�Ƃ���L�[�}�N�����쐬����D
�����K�Q�P���@�L�[�}�N����g�ݍ���
Range("B10:F12").Select Selection.Font.Name = "�l�r ����" Selection.ClearContents
�@�@�@�E����P�X���ō쐬�����L�[�}�N�����C����
�ā����K�Q�O���̃v���O�����ɑg�ݍ��ށD
�@�@�@�E�Z���iD1�j�u%�v�ʂ���L�[�}�N����
�@�@�@�@�@�@�쐬����D
�@�@�@�E�����K�Q�O���̃v���O�����ɑ����\�̂R�s�ڂ�\������v���O������lj�����D
�@�@�@�@���@ Range("D1").Select ��
Cells(1, 4).Select�@�c�@�Z�����w�肷��
�@�@�@�@�@�@�@�k�@�����K�Q�O���ɒlj�����v���O�����@�l
 For k = 2 To 6
For k = 2 To 6
If
Cells(11, k) = "�{" Then
Range("D1").Select: Selection.Copy
Cells(12, k).Select: ActiveSheet.Paste
 ElseIf Cells(11, k) = "�|" Then
ElseIf Cells(11, k) = "�|" Then
Range("E1").Select: Selection.Copy
Cells(12, k).Select: ActiveSheet.Paste
Else
Cells(12, k) = f3(Cells(10, k))
 End
If
End
If
Next k
�@�@�@����Q�O���@������0��
�@�@�@�Ȃ�l���d�����Ƃ�Ƃ���
�@�@�@�������\����������\����
��悤�Ƀv���O�����C����
��D
�@�@�@����Q�P���@���̂R����
�@�@�@�̑����\��\��������D
�@�@�@(1)�@![]()
(2)�@![]()
����A�������Ȋw�T��@���e�L�X�g14��
(2)
������
�ϐ��ɂ͐��l�ϐ��ƕ�����ϐ��̂Q��ނ̕ϐ�������܂��D������𑀍삷��
���Ƃ��ẮCLeft�CRight�CMid�Ȃǂ�����܂��D�����́C������̈ꕔ��
�������ł����C�����ł͂Q�̕������A�������܂��D
![]()
�@�@������![]() ��x���ƒ���
��x���ƒ��� ![]() �Ƃ�
�Ƃ�
�͂܂�镔�������̂悤�ɒ����`�ɍו�������
�ʐς����߂���@���敪���ϖ@�Ƃ����܂��D
 �@
�@
![]() �@�@
�@�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��������n�Ƃ���ƁC
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�ʐ� ![]() �@�ƂȂ�܂��D
�@�ƂȂ�܂��D
�������C![]() �C
�C![]()
�@�@�@�@�E���̒l��\������Z���Ƃ��āC���[�N�V�[�g�i�uWork�v�j���쐬����D
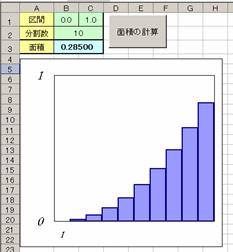 �@�@�@�@�E���[�N�V�[�g�i�u�敪���ϖ@�v�j��
�@�@�@�@�E���[�N�V�[�g�i�u�敪���ϖ@�v�j��
��ԁC�������C�ʐς��Z���ɐݒ肷��D
�@�@�@�@�E�}�N���{�^���i�u�ʐς̌v�Z�v�j���쐬
�@�@�@�@�@���āC����ɖʐς����߂�v���O����
�����蓖�Ă�D
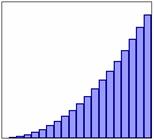
�@�@�@�@�E�O���t�E�B�U�[�h�Ńq�X�g�O������\
��������D
�@�@�@�@�@���̂Ƃ��C���̃O���t�̔ԍ����m�F��
![]() ��D
��D
�k�ʐς����߂�v���O�����l
Sub �ʐς̌v�Z() s = Cells(1, 2): e =
Cells(1, 3): n = Cells(2, 2) d = (e - s) / n Menseki = 0 For k = 1 To n
x = s + d * (k - 1)
Sheets("Work").Cells(k, 1) = x
Sheets("Work").Cells(k, 2) = f(x)
Menseki = Menseki + d * f(x) Next k Cells(3, 2) = Menseki: '�ʐ� b$ =
"=Work!R1C1:R" & Cells(2, 2) & "C1"
ActiveSheet.ChartObjects("�O���t 1").Activate
ActiveChart.SetSourceData Source:=Sheets("Work").Range(a$) End Sub Function
f(x) f = x ^ 2 End Function
�@�@
![]()

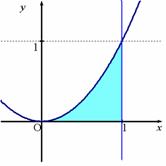
�@�@�@����Q�Q���@��
![]() ( n = �P�C2�C3�C�c )�@�̃O���t��x���ƒ���
( n = �P�C2�C3�C�c )�@�̃O���t��x���ƒ���
![]() �Ƃň͂܂�镔���̖ʐς����߁C�����̒l��n�ŕ\���Ƃǂ���
�Ƃň͂܂�镔���̖ʐς����߁C�����̒l��n�ŕ\���Ƃǂ���
�邩�𐄒肹��D

�@�@�@�@�@���@�ہ@��@��
�@����Q�Q���ɂ����āC��Ԃ� [0�Cx ]�Ƃ����Ƃ��̖ʐς�Sn(x)�Ƃ���Ƃ��C
Sn(x)��n��x��p���Ăǂ̂悤�ɕ\���邩�𐄒肵�C���̐��肪����������
���ؖ�����D