����A�������Ȋw�T��@���e�L�X�g21��
��1�́@��������
���P�@Mathematica����
Mathematica�́C���������\�t�g�ł��D���̃\�t�g�́C��ɁC�����̌v�Z���s��
�܂����C���̃O���t��}�`�̕`����s���܂��D�����Ŋw�K�������Ƃ𐔊w�̎�
 �Ƃł����p���Ă����܂����A�N�B���g�ł����p���@���l���Ă��������D
�Ƃł����p���Ă����܂����A�N�B���g�ł����p���@���l���Ă��������D
�܂��C������@�Ɋ���Ă��������D
�P�DMathematica�̊�{����
�܂��C���̃X�^�[�g�A�b�v�p���b�g��
�@�@�@10���Ԃ̃`���[�g���A��������Ă�����
���D23�y�[�W����܂����C�Ȃ��ɂ͓
�����̂��܂܂�Ă��܂����C��ʂ茩��
�����ĉ������D
�@���j���[�o�[������(H)�̂Ȃ�������ر�..(T)�ł��s���܂�.
�E �m�[�g�u�b�N
�N������ƍ��ɕ\�������E�C���h��
�m�[�g�u�b�N�Ƃ����C�����Ɏ��╶��
����͂���ƁC���ʂ������ɕ\������
�܂��D
�ŏ��́C���̃m�[�g�u�b�N�̖��O�́C
���̖���`�ƂȂ��Ă��܂��D���͂���
���̂�ۑ�����ƁC���O���t���܂��D
�E �p���b�g�ɂ���
���j���[�o�[�̃t�@�C��(F)�Ƀp���b�g(E)������܂��D
�����ɂ́C��������̓��͂��x���������̃p���b�g������܂��D���߂�
�����́C4 BasicInput�i��b�I�ȓ��́j��\�������Ă����Ƃ悢�ł��傤�D
�E  �Z���ɂ���
�Z���ɂ���
�m�[�g�u�b�N�ł́C�Z���Ƃ����P�ʂŎ��╶����
�Ǘ�����Ă��܂��D
�Z���̎�ނɂ́C����̓Z����C��o�̓Z����C
��^�C�g���Z����C��e�L�X�g�Z����Ȃǂ�����܂��D
�Z���̕\���`����StandardForm�i�W���`�j�ɂ��ĉ������D
����P�� �p���b�g�̓��͂Ɋ����D
�@AlgebraicManipulation�i�㐔�I����j��BasicInput�i��b�I�ȓ��́j��
 �Q�̃p���b�g���g���āC���̌v�Z������D
�Q�̃p���b�g���g���āC���̌v�Z������D
(1)
Sin[Pi/3]�@�̒l�����߂�D
(2)
![]() �@���v�Z����D
�@���v�Z����D
(3)
![]() �@��W�J����D
�@��W�J����D
(4)
![]() �@��������������D
�@��������������D
�@�@�@
|
�k����g�p����R�}���h�l �W�J�iExpand�j�C�@���������iFactor�j |
�����K�P���@���̌v�Z������D
(1)
Cos[Pi/4]�@�̒l�����߂�D
(2)
![]() �@���v�Z����D
�@���v�Z����D
(3)
![]() �@��W�J����D
�@��W�J����D
(4)
![]() �@��������������D
�@��������������D
(5)
![]() �@��ʕ�����D
�@��ʕ�����D
����A�������Ȋw�T��@���e�L�X�g22��
�E  �w���v�ɂ���
�w���v�ɂ���
Mathematica�̑�����@��
�R�}���h�A�g�ݍ��݊���
���Ē��ׂ�ɂ́A�w���v
���g���܂��D
����ɂ��Ċ���Ă�����
Mathematica�̊w�K���A�e
�ՂɂȂ�܂�.
�@�@
�E ![]() ���̃O���t
���̃O���t
�O���t��`���ɂ́CPlot�Ƃ����R�}���h���g���܂��D
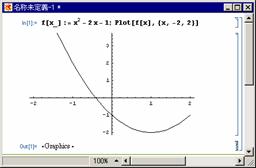
����Q���@![]() ��
��
�O���t��`���D
�@�@�@�@�@�@�@���@Plot�ɂ�,���낢���
�@�@�@�@�@�@�@�@�@�I�v�V����������܂��D
�I�v�V�������́C
Options[Plot3D]�Œ���
���܂��D
�I�v�V�����Ԃ́C�R���}�,��ŋ��܂��D
�k�����F�I�v�V���������ݒ�l�l
![]() ���၄�@
���၄�@
�@�@�@�@�@����P���@Plot�̂��ׂẴI�v�V�����ɂ��Ē��ׂ�D
�@
�����K�Q���@���̊��̃O���t��`���D
(1)�@![]() (2)�@
(2)�@![]()
(3)�@![]() (4)�@
(4)�@![]()
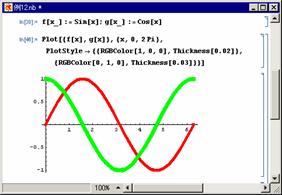 ����R���@2�̊��̃O���t��`��
����R���@2�̊��̃O���t��`��
�@�@���@2�̃O���t��`���ɂ́A
���X�g���g���܂��D
�@�@�@�@�����ʁo�@�p�̒��ɁC�`����
��������ׂ܂��D
�܂��C�I�v�V�����uPlotStyle�v
�ł́C�O���t�̐F�Ƒ������w��
���܂��D
�@�@�@�@�@�@���@RGBColor�ɂ���
�@�@�@�@�@�@�@�@[�@�@]�̒��ɐԁiRed�j�C�iGreen�j�C�iBlue�j�̏��ɁC0�`1�܂ł�
�@�@�@�@�@�@�@�@���l�ł��̋������w�肵�܂��B
�@�@���@�O���t�̐��̑����́CThickness[���l]�Ŏw�肵�܂��B
�����K�R���@���̎O�p���̃O���t���@0 �� x �� 2ð�@�͈̔͂œ������W
�ɕ`���D�������C�O���t�̐F�Ƒ����͎��R�Ƃ���B
�@�@(1)�@![]() �C
�C![]()
�@�@(2)�@![]() �C
�C![]() �@(3)�@
�@(3)�@![]() �C
�C![]() �C
�C![]()
�@�@�@�@�@����Q���@�� ![]() �̃O���t�́C��
�̃O���t�́C�� ![]() ��
��
�O���t��x�������ɂ����畽�s�ړ��������̂ł��邩�B���̂��Ƃ�
Mathematica�Ŋm���߂�B
����A�������Ȋw�T��@���e�L�X�g23��
�E �Ȑ��̔}��ϐ��\��
�}��ϐ��\���ŋȐ���`���ɂ́CParametricPlot�Ƃ����R�}���h���g���܂��D
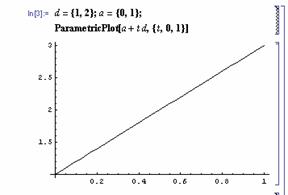
����S���@�����@![]() �@��`��
�@��`��
�@�@�����̕����x�N�g��![]() = ( 1 , 2 )
= ( 1 , 2 )
�ʂ�_A(
0 , 1 )�C![]() = ( 0 , 1 )
= ( 0 , 1 )
�@�@�x�N�g���������@![]()
�@�@�����ŕ\���ƁC( x, y ) = ( 0 , 1 ) + t( 1 , 2 ) = ( t , 2t + 1 )
�@�@�}��ϐ��\���@![]() �@�@�it���p�����[�^�܂��͔}��ϐ��Ƃ����j
�@�@�it���p�����[�^�܂��͔}��ϐ��Ƃ����j
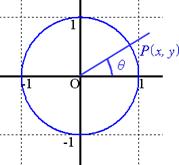
���Q�l���i���ȏ��u���w�b�vp.73�j
�@�@���_�𒆐S�Ƃ��āC���a1�̉~��
�}��ϐ��\���́C�~����̓_��P( x, y)�C
����OP��x���ƂȂ��p���ƂƂ���ƁC
x = cos�ƁCy = sin�Ɓ@�ƂȂ�̂ŁC
�@![]() �@�ƕ\����D
�@�ƕ\����D
�����K�S���@���̔}��ϐ��\���ŕ\����Ă���}�`��`���D
�@(1)�@![]() �@�@�i 0 �� t �� 2�� �j
�@�@�i 0 �� t �� 2�� �j
�@(2)�@![]() �@�@ �i 0 �� t �� 2�� �j
�@�@ �i 0 �� t �� 2�� �j
�@
�E �A���̃O���t
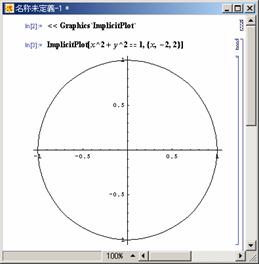 �A���Ƃ́C�~�̕������i
�A���Ƃ́C�~�̕������i![]() �j�̂悤��
�j�̂悤��![]() �Ƃ����`�ŕ\�������̂��Ƃł��D
�Ƃ����`�ŕ\�������̂��Ƃł��D
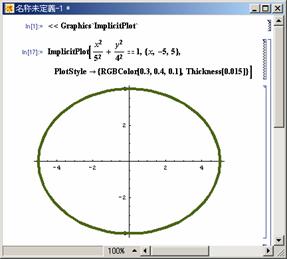
����T���@�~�@![]() �@��`��
�@��`��
���̊��̃O���t��`���ɂ́C
�uImplicitPlot�v�Ƃ����p�b�P�[�W
��ǂݍ��ޕK�v������܂��D

<<Graphics`ImplicitPlot`
���@�u�f�v�ł͂Ȃ��u`�v
�@�@= �͂Q������==�Ƃ���D
�����K�T���@���̕������ŕ\�����}�`��`���D
�@�@�@�@�@(1)�@![]() (2)�@
(2)�@![]()
�@(3)�@![]() (4)�@
(4)�@ ![]()
�E �s�����̕\���̈�
�s�����̕\���̈��\������ɂ́C�uInequalityGraphics�v�Ƃ����p�b�P�[�W
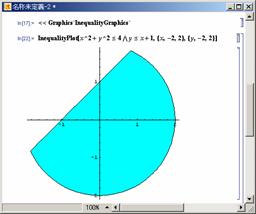 ��ǂݍ��ޕK�v������܂��D
��ǂݍ��ޕK�v������܂��D

<<Graphics`InequalityGraphics`
����U���@�s�����@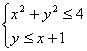 �@�`��
�@�`��
�@���@���ʕ�����`���ɂ́C�u![]() �v���g��
�v���g��
�܂��D
����A�������Ȋw�T��@���e�L�X�g24��
�Q�D�Q���Ȑ�
������![]() �̕\���Ȑ��̂����ŁC
�̕\���Ȑ��̂����ŁC![]() ��x�Cy��2�����̂��̂ɂ�
��x�Cy��2�����̂��̂ɂ�
�čl��D
����ʌ`���@![]()
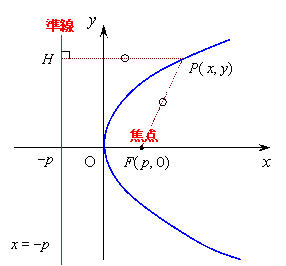
�E������
�@���� x = -p �ƒ�_F(p,0)�����
�������������_�̋O�Ղ����߂�ƁC
![]() �C
�C![]()
�@�@�@�@�@�@PH = PF ���
�@![]()
![]() �@�@�@�@�@�@���@�@
�@�@�@�@�@�@���@�@![]() �@�@���W���`��
�@�@���W���`��
����V���@�œ_(1�C0)�C���� ![]() �̕������̕����������߂�D
�̕������̕����������߂�D
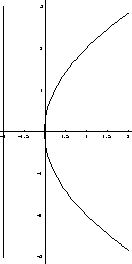 �܂��C�����ƕ������̊T�`�������D�@
�܂��C�����ƕ������̊T�`�������D�@

�����K�U���@���̕������̏œ_�̍��W�Ə����̕�����
�����߁C�����ƕ������̊T�`�������D
�@�@�@�@�@(1)�@![]() (2)�@
(2)�@![]()
�@(3)�@![]() (4)�@
(4)�@![]()
�@
 �E�ȉ~
�E�ȉ~
2��_F( c�C0)�CF�f( -c, 0)����̋����̘a����� 2a
�ł���_�̋O�Ղ����߂�ƁC
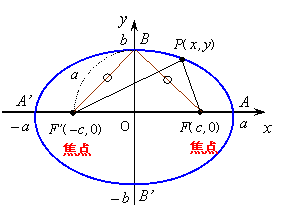 PF �{ PF�f �� 2a�@���C
PF �{ PF�f �� 2a�@���C
![]()
����āC![]()
���ӂ�2�悵�Đ�������ƁC
![]()
�@�@�@������x���ӂ�2�悵�Đ�������ƁC
�@�@�@�@![]()
�@�@�@�@![]() �i���Ȃ킿�C
�i���Ȃ킿�C![]() �j�Ƃ����ƁC
�j�Ƃ����ƁC
4�̓_A�CA�f�CB�CB�f �����_�Ƃ����C ����A�fA�������C����B�fB���Z���Ƃ����D
 �@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@![]() �@�@���W���`��
�@�@���W���`��
 ����W���@2��_(4�C0)�C(-4�C0)�����
����W���@2��_(4�C0)�C(-4�C0)�����
�����̘a��10�ł���ȉ~�̕���������
�߂�D�܂��C�ȉ~�̊T�`�������D�@
�����K�V���@���̑ȉ~�̏œ_�̍��W��
�����C�Z���̒��������߁C�ȉ~
�̊T�`�������D
�@�@�@�@�@(1)�@ ![]()
�@(2)�@![]()
�@(3)�@![]()
����A�������Ȋw�T��@���e�L�X�g25��
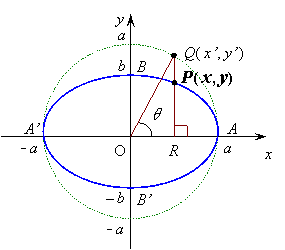
�E�ȉ~�̔}��ϐ��\��
�@���aa�̉~����̓_Q(x�f�Cy�f)��
�@�}��ϐ��\����
![]() �Ƃ��C
�Ƃ��C
�@����QR�Ƒȉ~
![]() �Ƃ�
�Ƃ�
�@��_��P(x,y)�Ƃ���ƁC
�@![]() ���C
���C
�@![]() �ƂȂ�C
�ƂȂ�C
�@�Ƃ̒l���l������ƁC![]() �ƂȂ�D
�ƂȂ�D

�@����āC�@�@![]() �@�@�@���ȉ~�̔}��ϐ��\����
�@�@�@���ȉ~�̔}��ϐ��\����
�@�@�@�@����R���@��̐}�ɂ����āC�� QR�FPR �͈��ł��邱�Ƃ������D
�܂��C���̔�͂�����ł��邩�D
����X���@�œ_��(0�C4)�C(0�C-4)�ŁC2�œ_����̋����̘a��10
�ł���ȉ~�̔}��ϐ��\���Ƒȉ~�̕����������߂�D
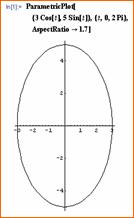
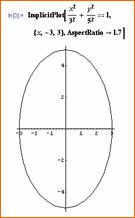 �܂��C���̊T�`�������D
�܂��C���̊T�`�������D
�����K�W���@���̑ȉ~�̔}��ϐ�
�\�������߁C���̊T�`�������D
�@�@�@�@�@(1)�@![]()
�@�@�@�@�@(2)�@![]()
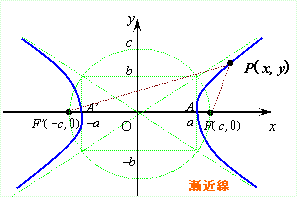 �E�o�Ȑ�
�E�o�Ȑ�
2��_F( c�C0)�CF�f( -c, 0)����̋����̍���
��� 2a�ł���_�̋O�Ղ����߂�ƁC
![]() �@���C
�@���C
![]()
-c
�@�@�@����āC
![]()
���ӂ�2�悵�Đ�������ƁC ![]()
������x���ӂ�2�悵�Đ�������ƁC![]()
![]() �i���Ȃ킿�C
�i���Ȃ킿�C![]() �j�Ƃ����ƁC
�j�Ƃ����ƁC
�_A�CA�f �����_�Ƃ����C����A�fA���厲�C2����
![]() ���Q�ߐ��Ƃ����D
���Q�ߐ��Ƃ����D
![]() �@�@���W���`��
�@�@���W���`��
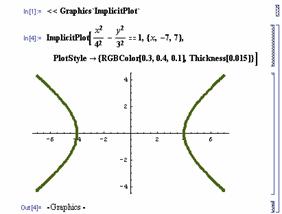 ����S���@
����S���@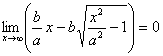 �@�������D
�@�������D
����10���@2��_(5�C0)�C(-5�C0)�����
�����̍���8�ł���o�Ȑ��̕�����
�����߂�D�܂��C���̊T�`�������D�@
�����K11���@���̑o�Ȑ��̏œ_�̍��W�Ǝ厲
�̒��������߁C�o�Ȑ��̊T�`�������D
�@�@�@�@(1)�@ ![]() �@(2)�@
�@(2)�@ ![]()